[스터디/알고리즘] 이것이 코딩테스트다 CH7.이진 탐색
CH7-1. 범위를 반씩 좁혀가는 탐색
+) 이코테 교재 깃허브
순차 탐색이란?
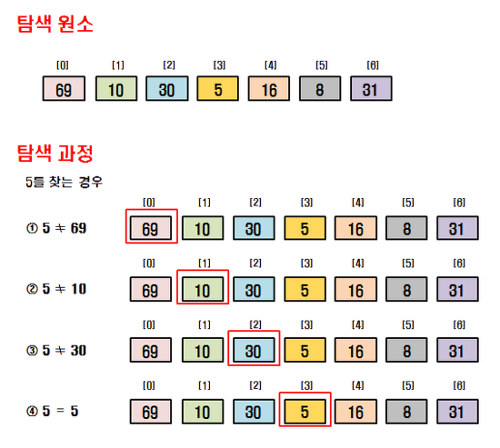
리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법.
- 정렬되지 않은 리스트에서 데이터를 찾아야할 때 사용
[사용 예시]
- 리스트에 특정 값의 원소가 있는가?
-
리스트에서 특정한 값을 가지는 원소의 개수는 몇인가?
[구현 코드]
#include <bits/stdc++.h>
using namespace std;
// 순차 탐색 소스코드 구현
int sequantialSearch(int n, string target, vector<string> arr) {
// 각 원소를 하나씩 확인하며
for (int i = 0; i < n; i++) {
// 현재의 원소가 찾고자 하는 원소와 동일한 경우
if (arr[i] == target) {
return i + 1; // 현재의 위치 반환 (인덱스는 0부터 시작하므로 1 더하기)
}
}
return -1; // 원소를 찾지 못한 경우 -1 반환
}
int n; // 원소의 개수
string target; // 찾고자 하는 문자열
vector<string> arr;
int main(void) {
cout << "생성할 원소 개수를 입력한 다음 한 칸 띄고 찾을 문자열을 입력하세요." << '\n';
cin >> n >> target;
cout << "앞서 적은 원소 개수만큼 문자열을 입력하세요. 구분은 띄어쓰기 한 칸으로 합니다." << '\n';
for (int i = 0; i < n; i++) {
string x;
cin >> x;
arr.push_back(x);
}
// 순차 탐색 수행 결과 출력
cout << sequantialSearch(n, target, arr) << '\n';
}
- 단위연산: 비교 (arr[i] == target)
- 최악 시간 복잡도: O(n)
이진 탐색이란?
찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는 과정
- 정렬되어 있는 리스트에서 데이터를 찾아야할 때 사용
[사용 예시]
-
이진 탐색 트리
-
변수 3개 이용 : 시작점, 끝점, 중간점
-

[구현 코드]
- 재귀함수의 이용 : 이진탐색은 문제 자체가 재귀적이다.
#include <bits/stdc++.h>
using namespace std;
// 이진 탐색 소스코드 구현(재귀 함수)
int binarySearch(vector<int>& arr, int target, int start, int end) {
if (start > end) return -1;
int mid = (start + end) / 2;
// 찾은 경우 중간점 인덱스 반환
if (arr[mid] == target) return mid;
// 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
else if (arr[mid] > target) return binarySearch(arr, target, start, mid - 1);
// 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else return binarySearch(arr, target, mid + 1, end);
}
int n, target;
vector<int> arr;
int main(void) {
// n(원소의 개수)와 target(찾고자 하는 값)을 입력받기
cin >> n >> target;
// 전체 원소 입력받기
for (int i = 0; i < n; i++) {
int x;
cin >> x;
arr.push_back(x);
}
// 이진 탐색 수행 결과 출력
int result = binarySearch(arr, target, 0, n - 1);
if (result == -1) {
cout << "원소가 존재하지 않습니다." << '\n';
}
else {
cout << result + 1 << '\n';
}
}
- 반복문 이용 : 재귀함수는 모두 반복문으로 표현 가능하다.
#include <bits/stdc++.h>
using namespace std;
// 이진 탐색 소스코드 구현(반복문)
int binarySearch(vector<int>& arr, int target, int start, int end) {
while (start <= end) {
int mid = (start + end) / 2;
// 찾은 경우 중간점 인덱스 반환
if (arr[mid] == target) return mid;
// 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
else if (arr[mid] > target) end = mid - 1;
// 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else start = mid + 1;
}
return -1;
}
int n, target;
vector<int> arr;
int main(void) {
// n(원소의 개수)와 target(찾고자 하는 값)을 입력 받기
cin >> n >> target;
// 전체 원소 입력 받기
for (int i = 0; i < n; i++) {
int x;
cin >> x;
arr.push_back(x);
}
// 이진 탐색 수행 결과 출력
int result = binarySearch(arr, target, 0, n - 1);
if (result == -1) {
cout << "원소가 존재하지 않습니다." << '\n';
}
else {
cout << result + 1 << '\n';
}
}
- 단위연산: 비교
- 최악 시간 복잡도: O(log n)
- 원소가 평균적으로 절반이 줄어든다.
-
재귀적 방법은 중복 수행이 발생하기 때문에 수행 속도가 반복문을 이용한 것보다 느리다.
- 탐색 범위가 크고 정렬되어 있을 때, 이진 탐색 알고리즘을 이용하는 것이 좋다. 이와 반대라면, 순차 알고리즘을 이용하자.
이미지출처:https://sw-tech.tistory.com/entry/%ED%83%90%EC%83%89%EC%88%9C%EC%B0%A8-%ED%83%90%EC%83%89 , https://minhamina.tistory.com/127