CH5-2. 탐색 알고리즘, DFS/BFS의 학습

그래프의 기본 구조

• 노드, 간선
• 탐색 : 하나의 노드를 시작으로 다수의 노드를 방문하는 것.
• 프로그래밍에서 그래프를 표현하는 2가지 방식
  • 인접 행렬 : 2차열 배열로 그래프의 연결 관계를 표현
  • 인접 리스트 : 리스트로 그래프의 연결 관계를 표현

인접 행렬 방식

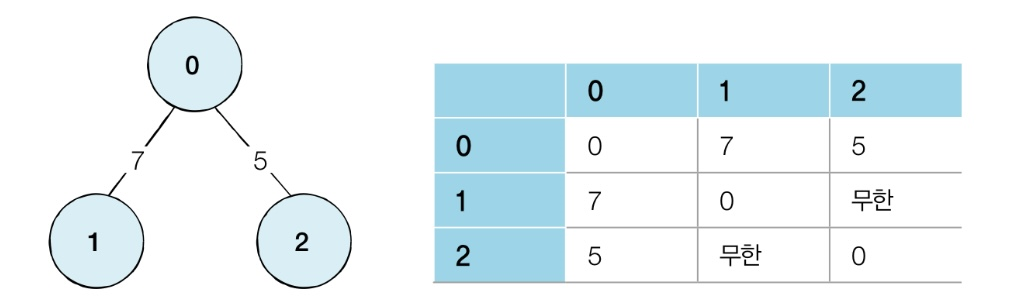
• 2차원 배열에 각 노드가 연결된 형태를 기록하는 방식
• 연결되어 있지 않은 노드끼리는 무한의 비용으로 선언한다.
  • 코드에서 999999999 등의 값으로 넣는데, 그 이유는 논리적으로 정답이 될 수 없는 큰 값이기 때문이다.
• 

#include <iostream>
#define INF 999999999 // 무한의 비용 선언

using namespace std;

// 2차원 리스트를 이용해 인접 행렬 표현
int graph[3][3] = {
    {0, 7, 5},
    {7, 0, INF},
    {5, INF, 0}
};

int main(void) {
    // 그래프 출력
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 3; j++) {
            cout << graph[i][j] << ' ';
        }
        cout << '\n';
    }
}

인접 리스트 방식

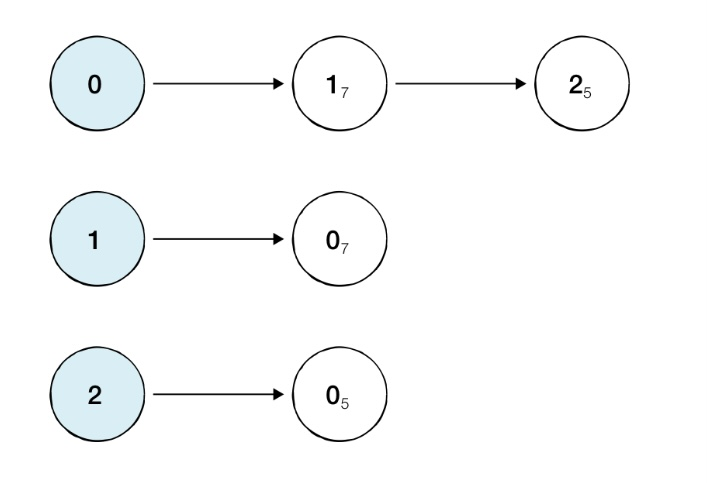
• 연결 리스트에 각 노드가 연결된 형태를 기록하는 방식
• C++과 자바는 별도의 연결 리스트 기능의 표준 라이브러리를 제공한다. (+파이썬은 append()와 메소드 제공)
• 

#include <iostream>
#include <vector>
using namespace std;

// 행(Row)이 3개인 인접 리스트 표현
vector<pair<int, int> > graph[3];

int main(void) {
    // 노드 0에 연결된 노드 정보 저장 {노드, 거리}
    graph[0].push_back({ 1, 7 });
    graph[0].push_back({ 2, 5 });

    // 노드 1에 연결된 노드 정보 저장 {노드, 거리}
    graph[1].push_back({ 0, 7 });

    // 노드 2에 연결된 노드 정보 저장 {노드, 거리}
    graph[2].push_back({ 0, 5 });

    // 그래프 출력
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < graph[i].size(); j++) {
            cout << '(' << graph[i][j].first << ',' << graph[i][j].second << ')' << ' ';
        }
        cout << '\n';
    }
}

인접 행렬 방식 VS 인접 리스트

• 메모리 측면
  • 인접 행렬의 경우, 모든 관계를 저장하기에 노드 개수가 많을수록 메모리가 불필요하게 낭비된다.
  • 인접 리스트는 연결된 정보만 저장하기 때문에 메모리를 효율적으로 사용한다.
• 속도 측면
  • 인접 리스트는 인접 행렬 방식에 비해 특정한 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느리다.
  • 인접 리스트는 차례대로 확인, 연결된 인접 노드를 모두 탐색하는 순회탐색이 필요하다.

DFS (Depth-First Search)

깊이 우선 탐색이라고도 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘.

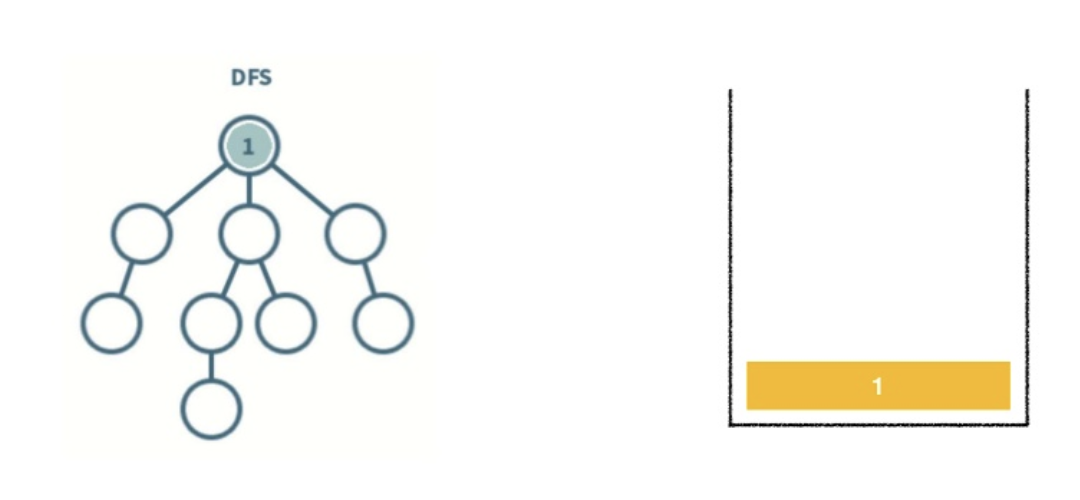
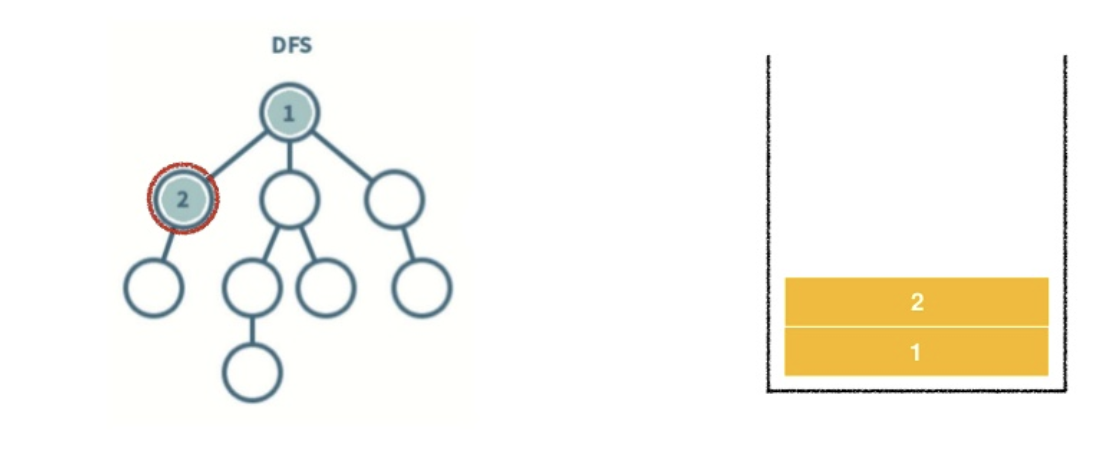
• 스택 자료구조를 이용한다.
  1. 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
  2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리를 한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
  3. 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.

*방문처리? 스택에 한 번 삽입되어 처리된 노드가 다시 삽입되지 않게 체크하는 것. (방문처리=스택에 넣기)

• 인접한 노드가 여러 개라면 번호가 낮은 순서부터 처리한다.
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 

• 

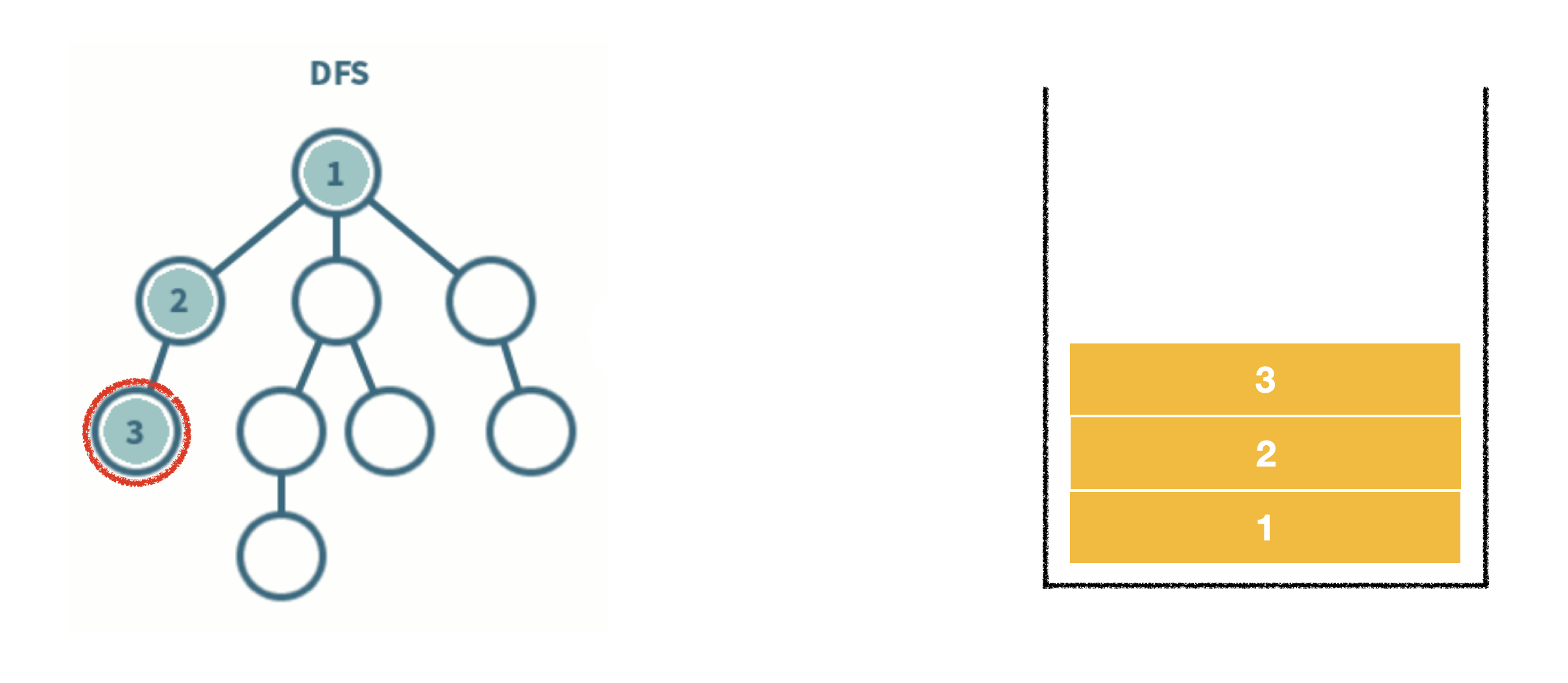
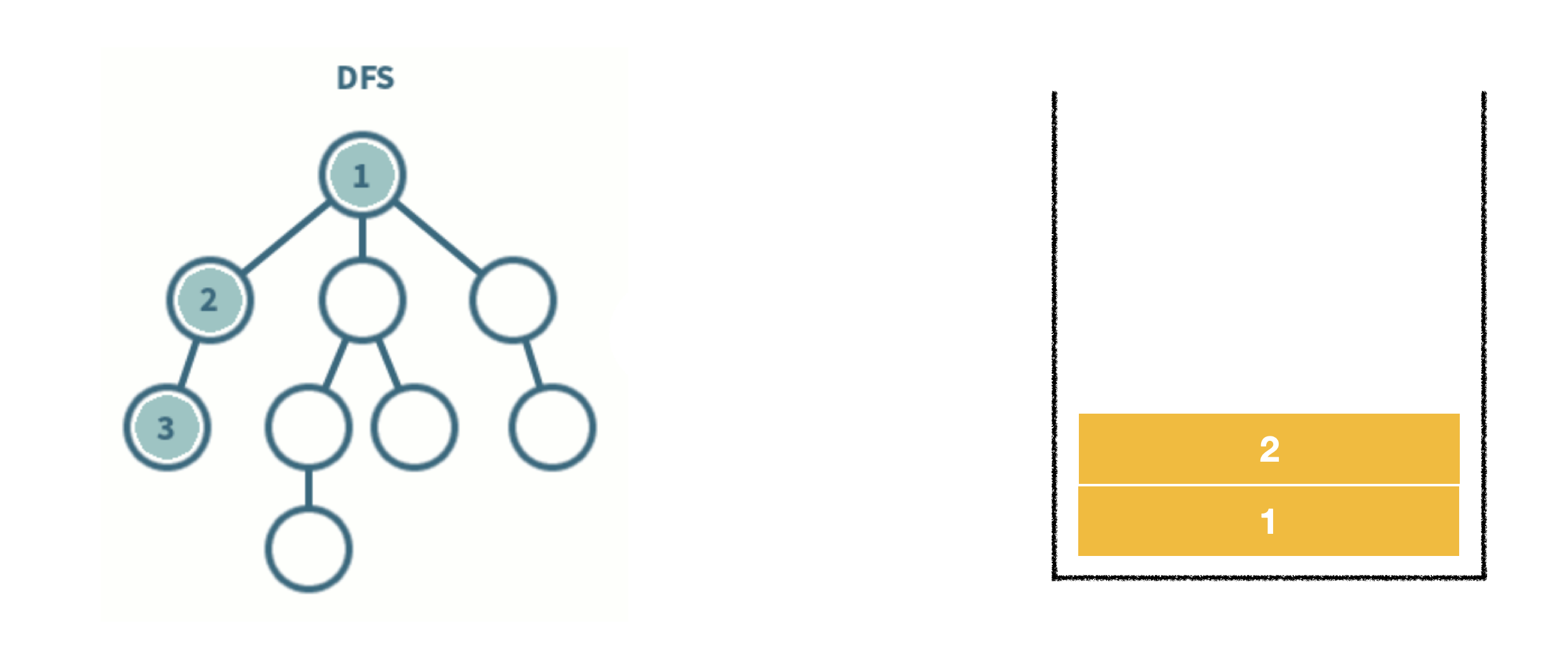
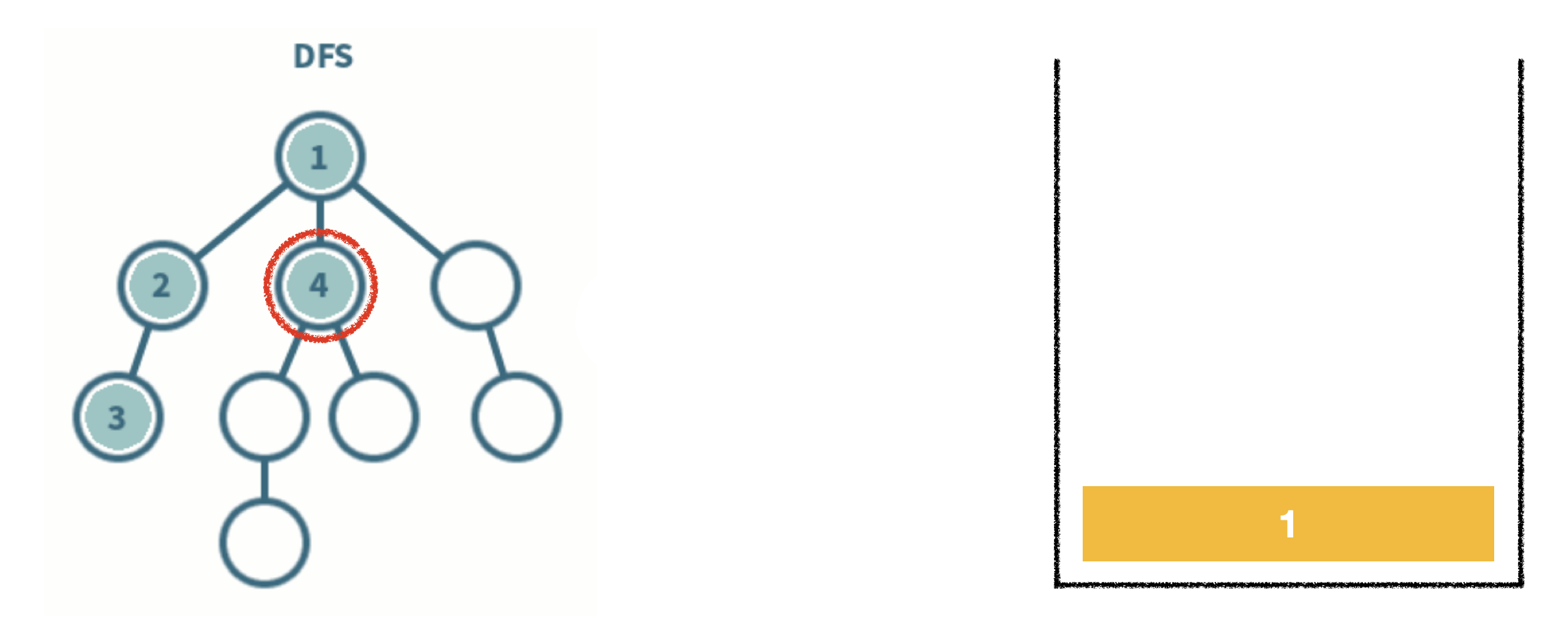
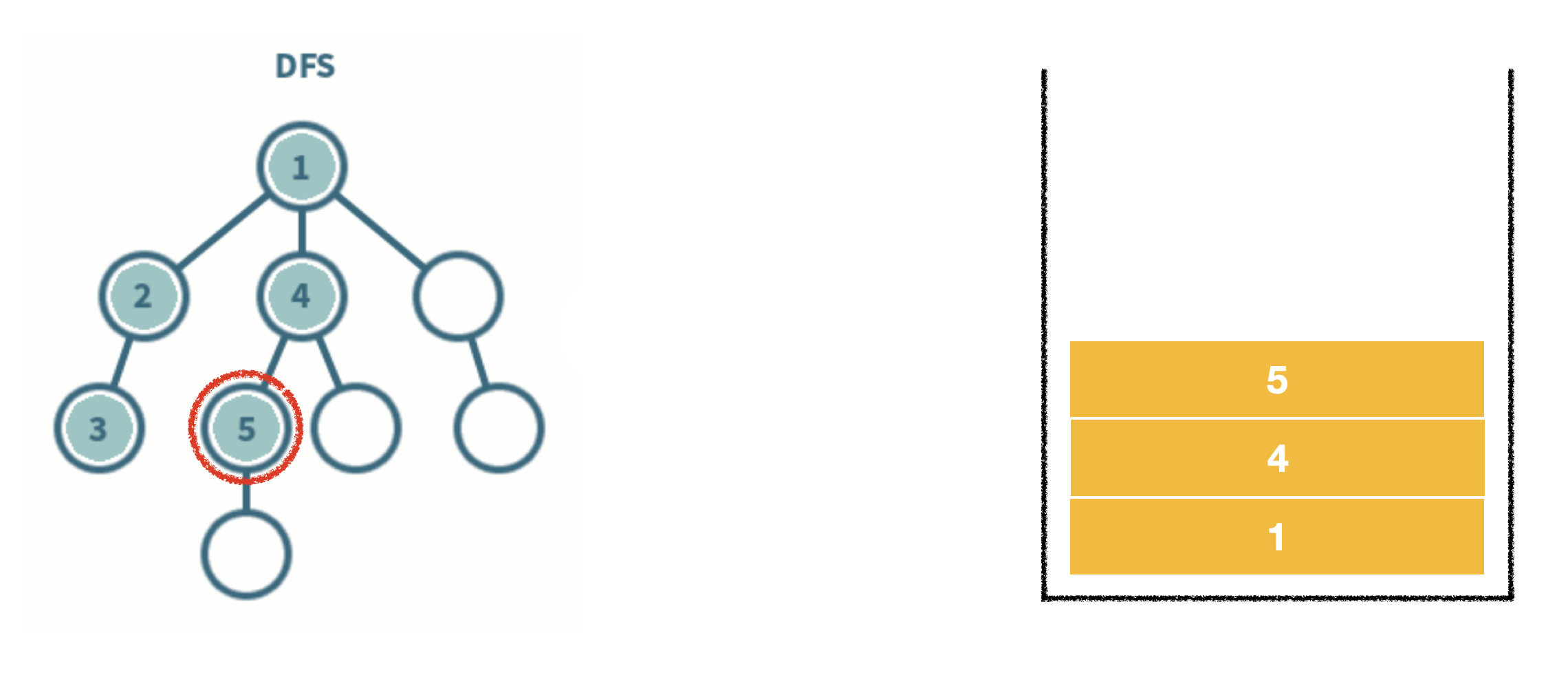
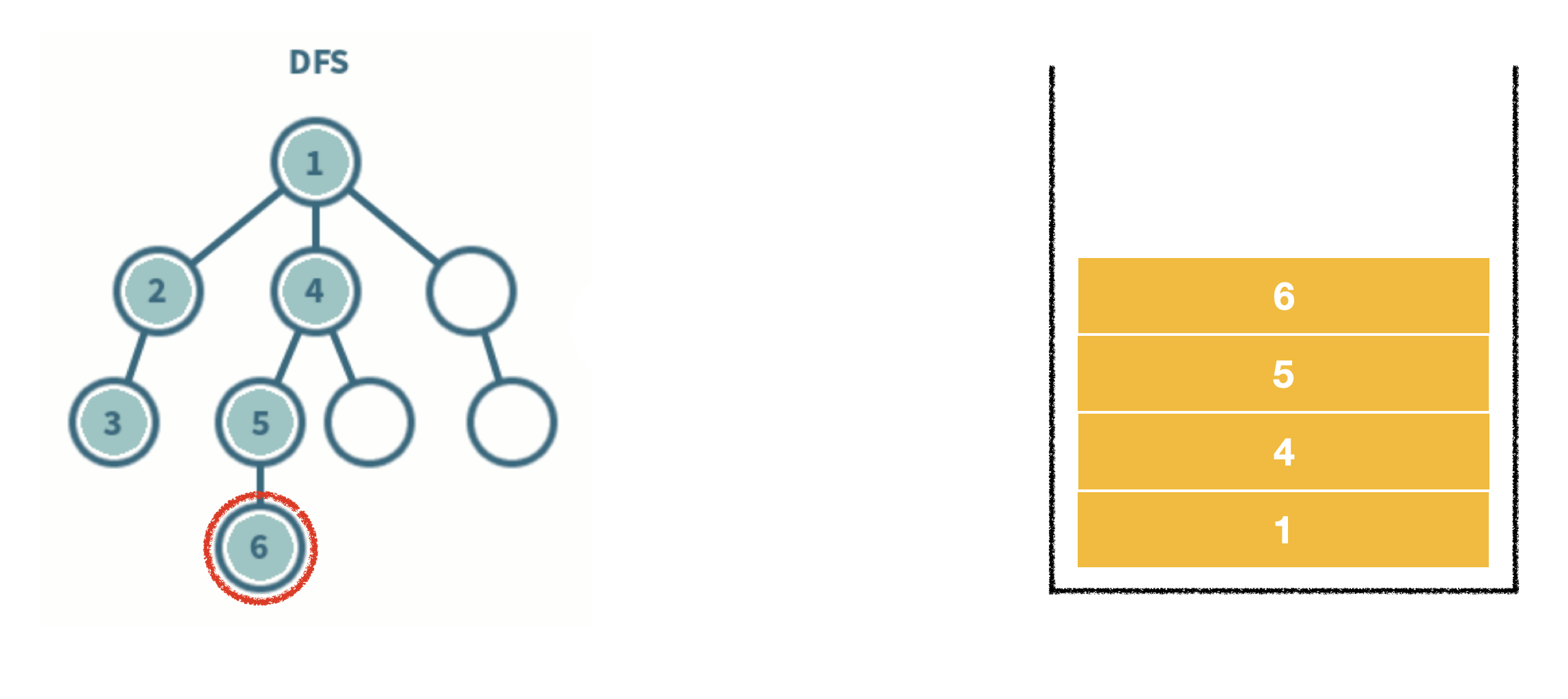
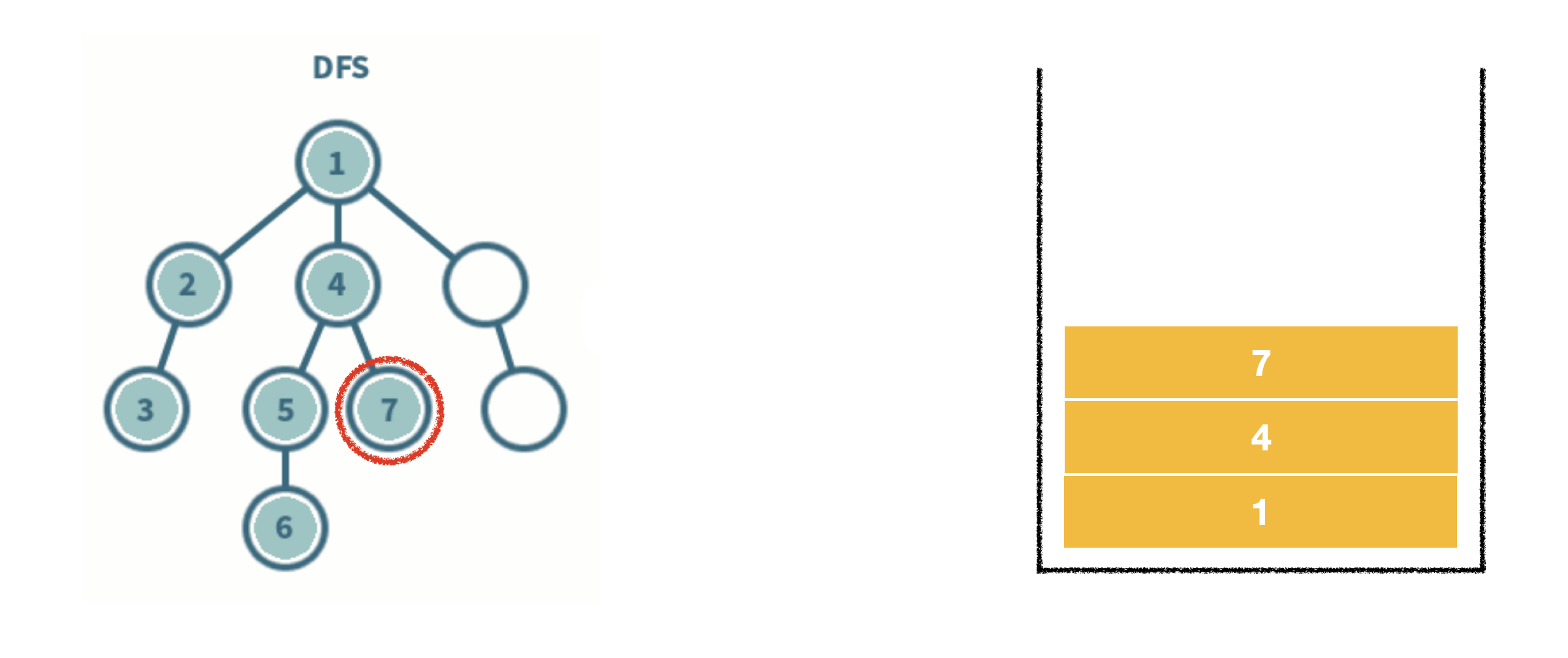
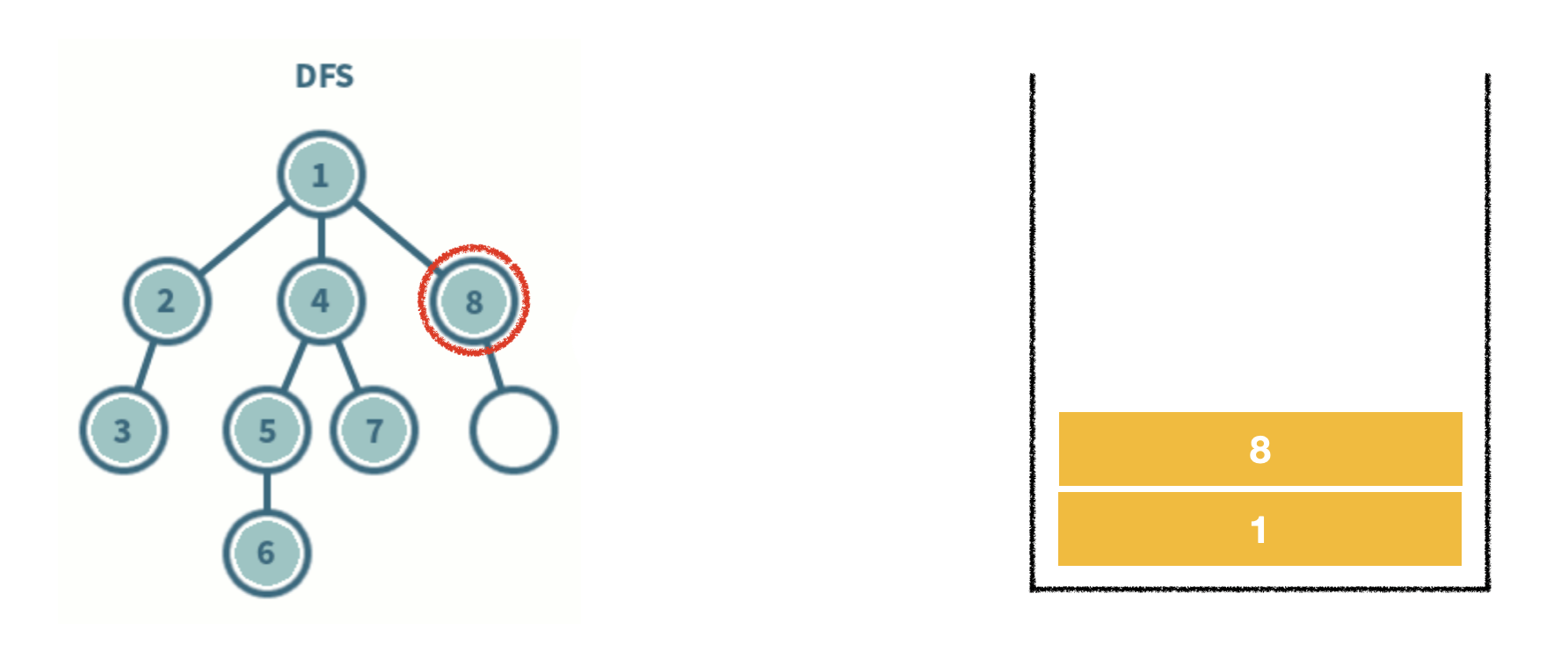
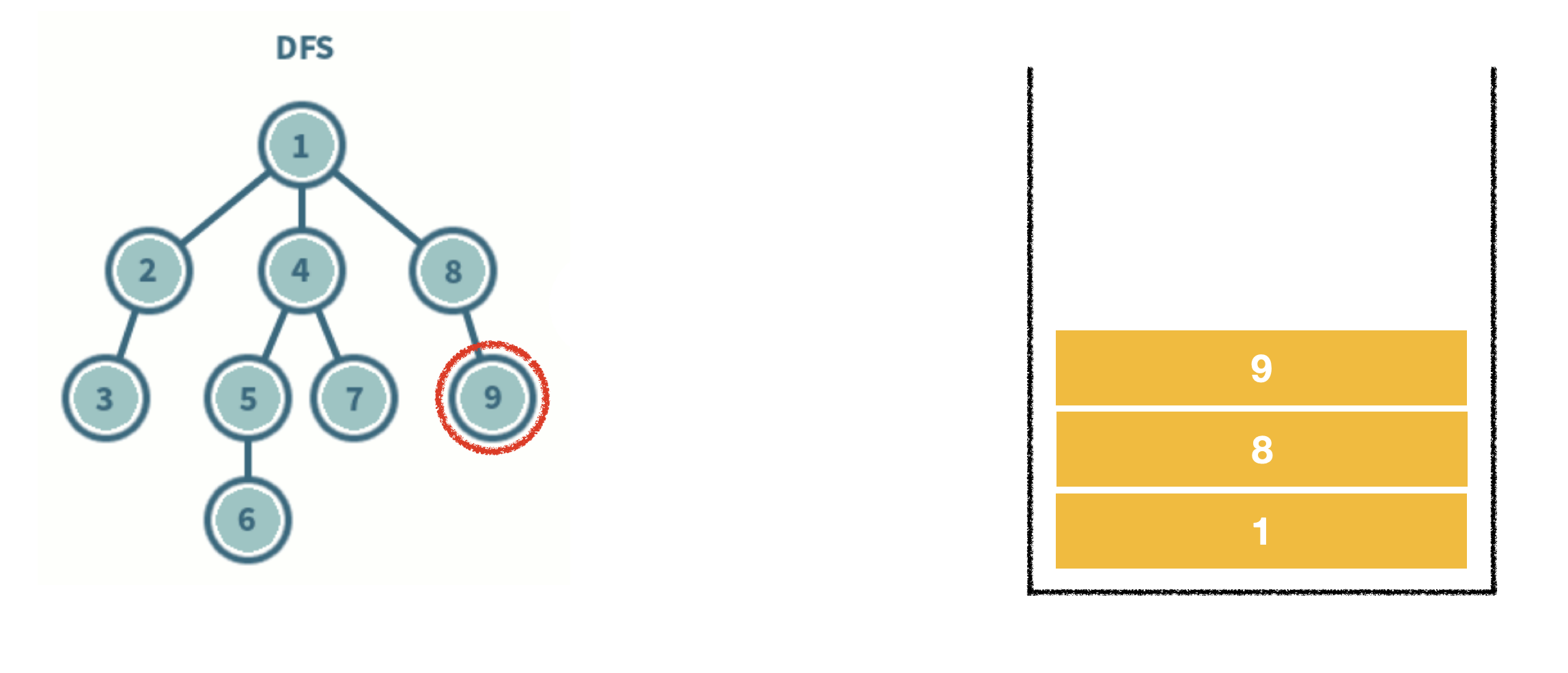
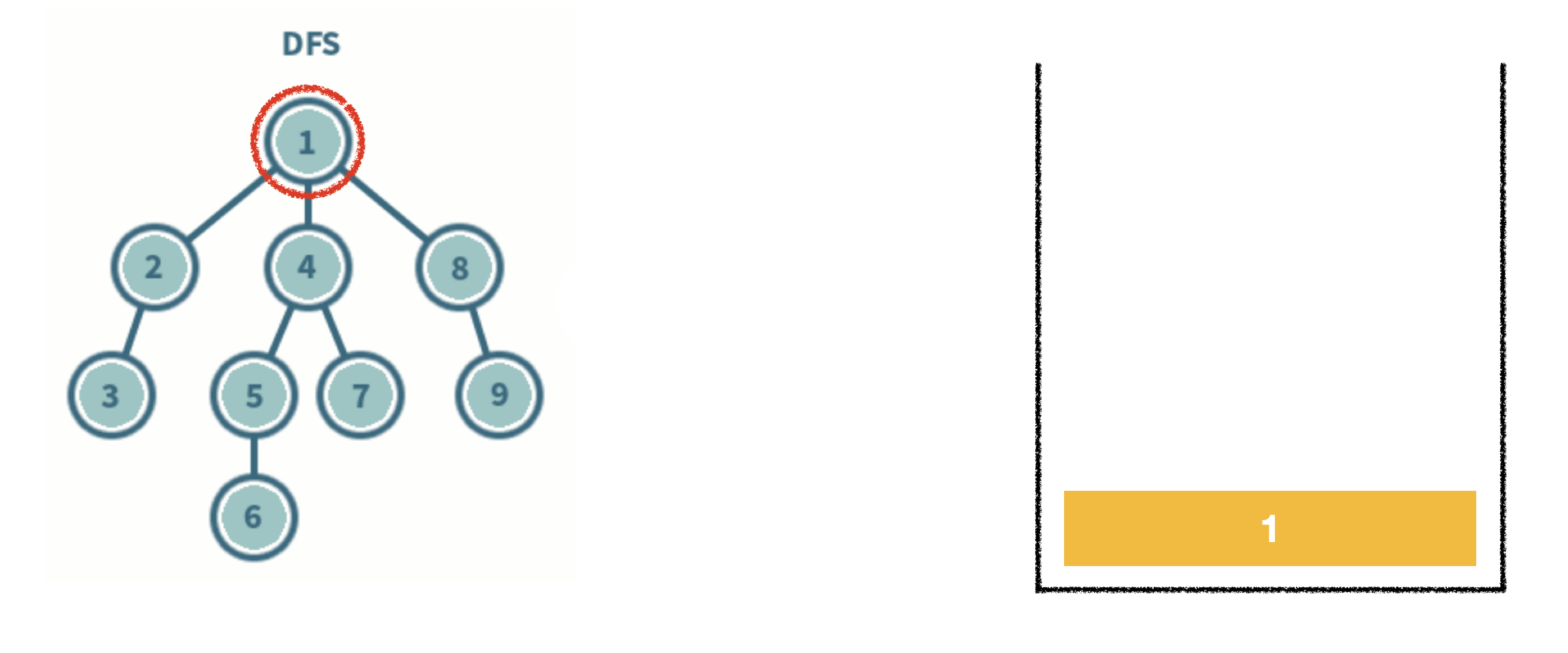
• 코드로 구현할 , 스택을 재귀 함수로 이용.

#include <iostream>
#include <vector>
using namespace std;

bool visited[9];
vector<int> graph[9];

// DFS 함수 정의
void dfs(int x) {
    // 현재 노드를 방문 처리
    visited[x] = true;
    cout << x << ' ';
    // 현재 노드와 연결된 다른 노드를 재귀적으로 방문
    for (int i = 0; i < graph[x].size(); i++) {
        int y = graph[x][i];
        if (!visited[y]) dfs(y);
    }
}
int main(void) {
    // 노드 1에 연결된 노드 정보 저장 
    graph[1].push_back(2);
    graph[1].push_back(3);
    graph[1].push_back(8);

    // 노드 2에 연결된 노드 정보 저장 
    graph[2].push_back(1);
    graph[2].push_back(7);

    // 노드 3에 연결된 노드 정보 저장 
    graph[3].push_back(1);
    graph[3].push_back(4);
    graph[3].push_back(5);

    // 노드 4에 연결된 노드 정보 저장 
    graph[4].push_back(3);
    graph[4].push_back(5);

    // 노드 5에 연결된 노드 정보 저장 
    graph[5].push_back(3);
    graph[5].push_back(4);

    // 노드 6에 연결된 노드 정보 저장 
    graph[6].push_back(7);

    // 노드 7에 연결된 노드 정보 저장 
    graph[7].push_back(2);
    graph[7].push_back(6);
    graph[7].push_back(8);

    // 노드 8에 연결된 노드 정보 저장 
    graph[8].push_back(1);
    graph[8].push_back(7);

    dfs(1);
}

• 데이터 개수가 N인 경우 O(N) 소요.

BFS (Breadth-First Search)

너비 우선 탐색이라고도 부르며, 그래프에서 가까운 노드부터 탐색하는 알고리즘.

• 큐 자료구조를 이용한다.
  1. 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
  2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 한다.
  3. 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.
• 인접한 노드가 여러 개라면 숫자가 낮은 순서부터 처리한다.
• 
• 
• 
• 

• 

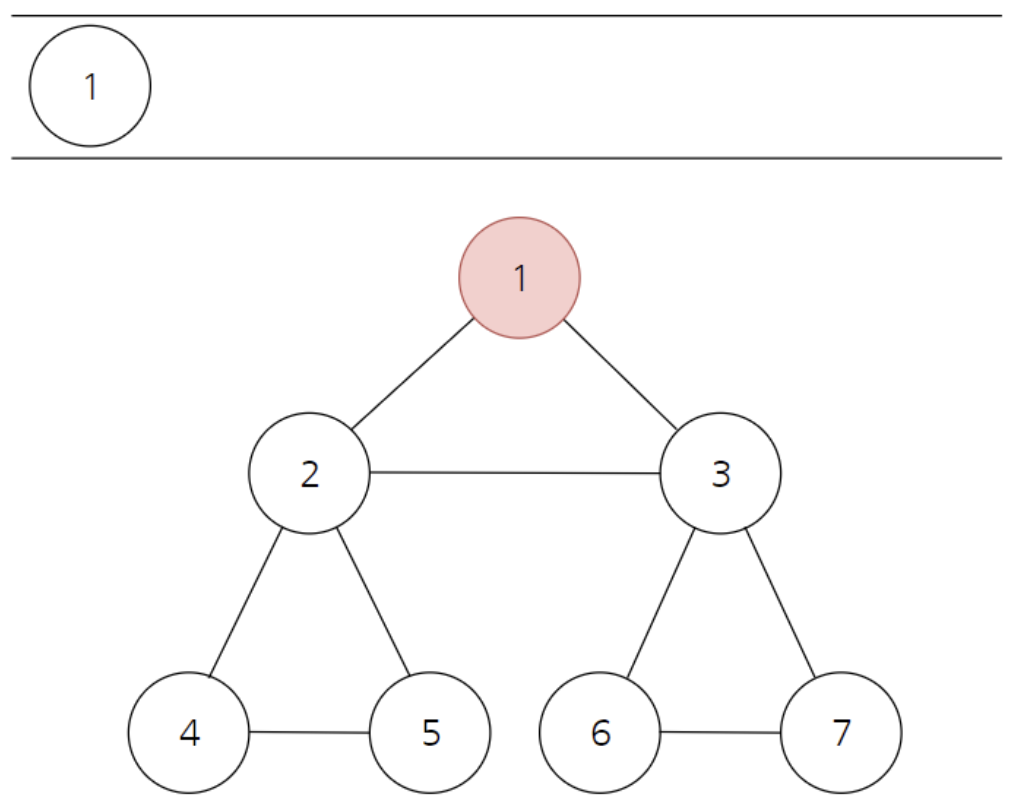
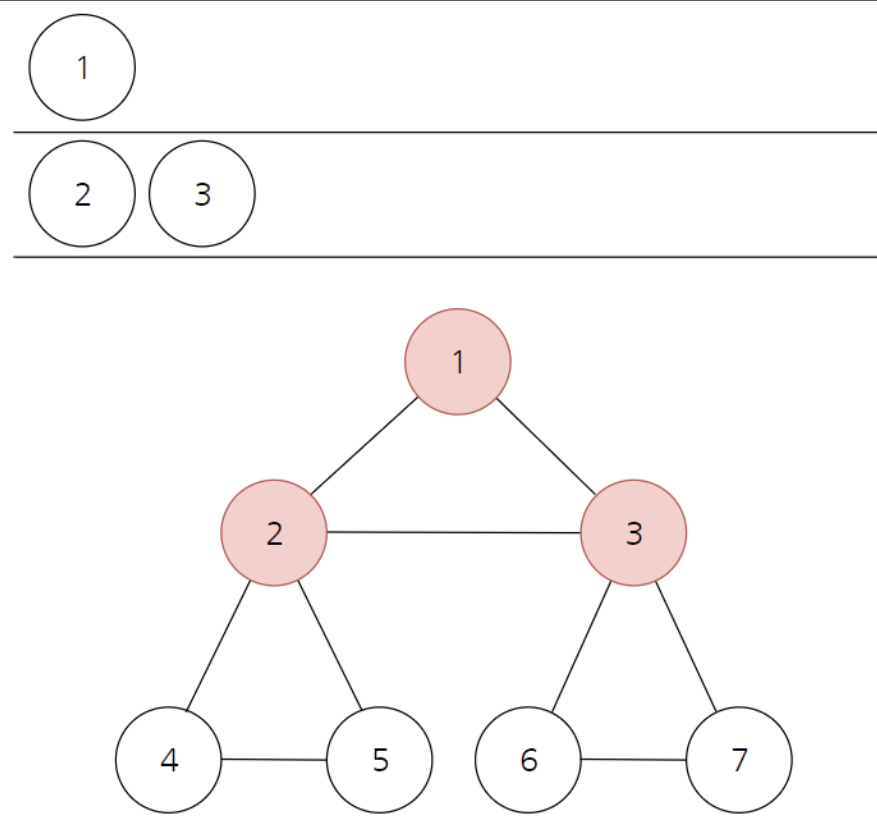
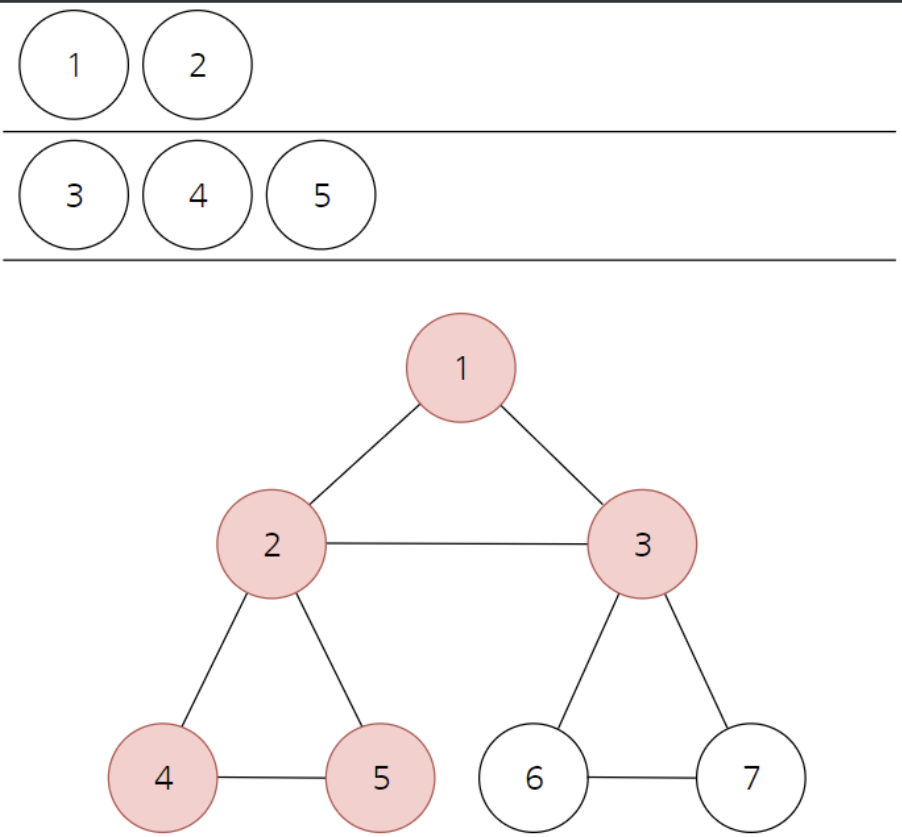
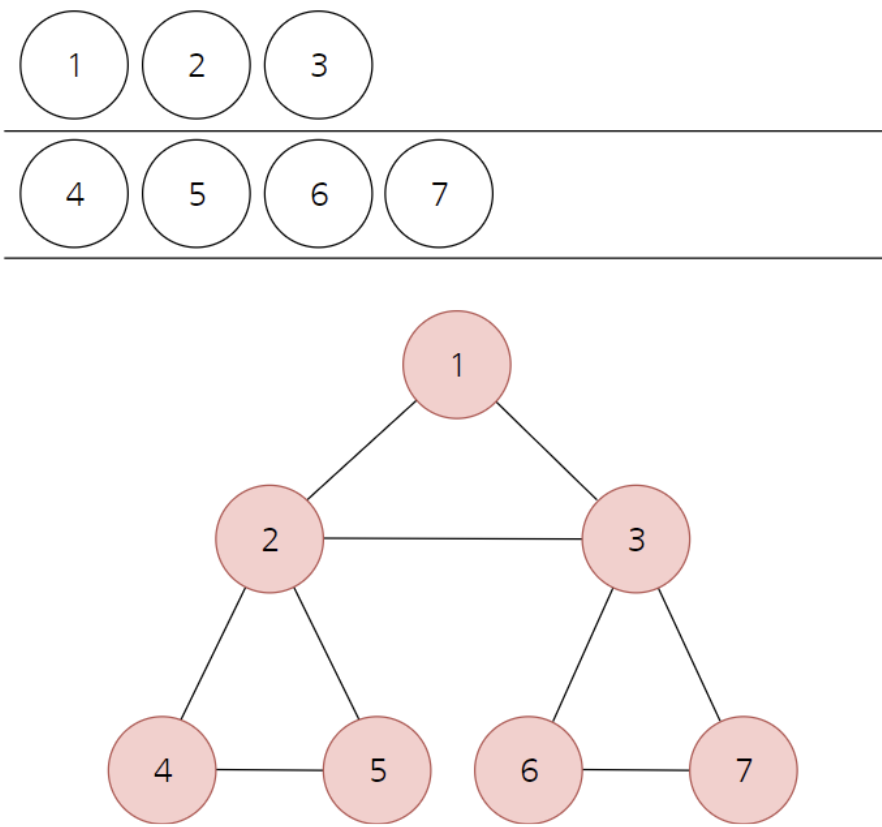
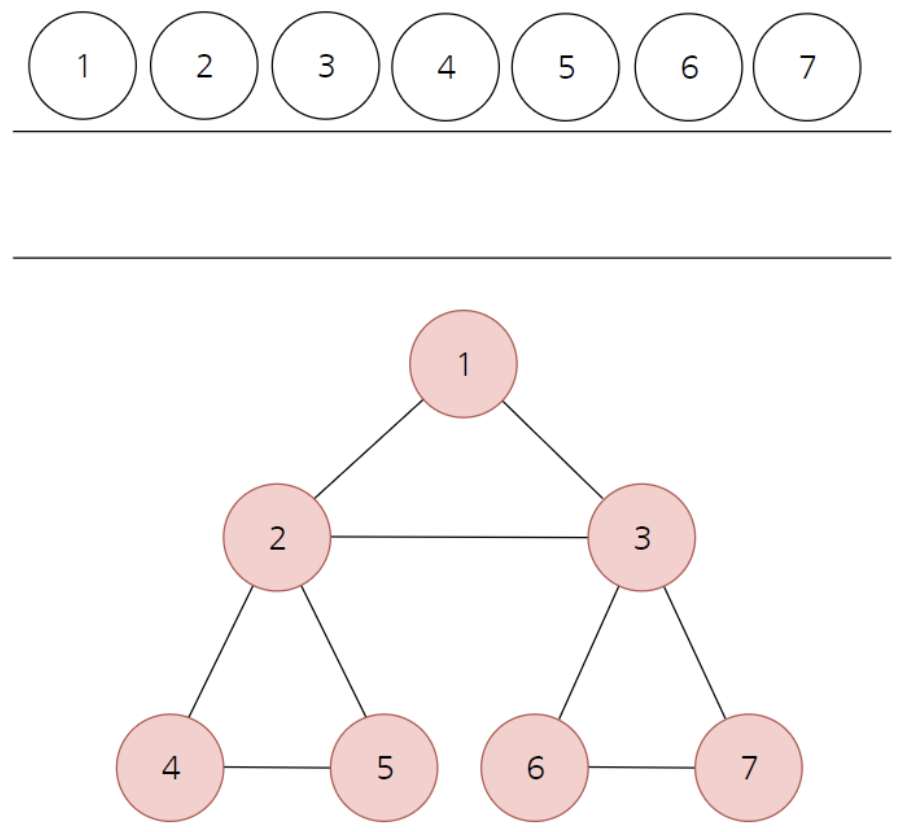
• 코드로 구현할 때, queue 이용. ```c++ #include #include #include using namespace std;

bool visited[9]; vector graph[9];

// BFS 함수 정의 void bfs(int start) { queue q; q.push(start); // 현재 노드를 방문 처리 visited[start] = true; // 큐가 빌 때까지 반복 while (!q.empty()) { // 큐에서 하나의 원소를 뽑아 출력 int x = q.front(); q.pop(); cout << x << ' '; // 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입 for (int i = 0; i < graph[x].size(); i++) { int y = graph[x][i]; if (!visited[y]) { q.push(y); visited[y] = true; } } } }

int main(void) { // 노드 1에 연결된 노드 정보 저장 graph[1].push_back(2); graph[1].push_back(3); graph[1].push_back(8);

// 노드 2에 연결된 노드 정보 저장 
graph[2].push_back(1);
graph[2].push_back(7);

// 노드 3에 연결된 노드 정보 저장 
graph[3].push_back(1);
graph[3].push_back(4);
graph[3].push_back(5);

// 노드 4에 연결된 노드 정보 저장 
graph[4].push_back(3);
graph[4].push_back(5);

// 노드 5에 연결된 노드 정보 저장 
graph[5].push_back(3);
graph[5].push_back(4);

// 노드 6에 연결된 노드 정보 저장 
graph[6].push_back(7);

// 노드 7에 연결된 노드 정보 저장 
graph[7].push_back(2);
graph[7].push_back(6);
graph[7].push_back(8);

// 노드 8에 연결된 노드 정보 저장 
graph[8].push_back(1);
graph[8].push_back(7);

bfs(1); } ```

• 데이터 개수가 N인 경우 O(N) 소요.
• 실제 수행시간이 DFS보다 좋다.

이미지 출처:https://velog.io/@sohi_5/algorithmDFS , https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=ndb796&logNo=221230944971 ,